Design Calculator Using Turing Machine and Jflap

Turing Machines: Examples

Last modified: Sep 20, 2021

Abstract

Practice designing and working with Turing machines.

1 JFlap

1. Review the Turing machines section of the Tutorial.

2. Construct the TM from examples 8.2/8.3. Use it to solve Exercise 8.2.1.

3. Construct your own Turing machine to solve Exercise 8.2.2a. (Note that this language is not a CFL.)

2 New Ways to Solve Old Problems

2.1 Contains 101

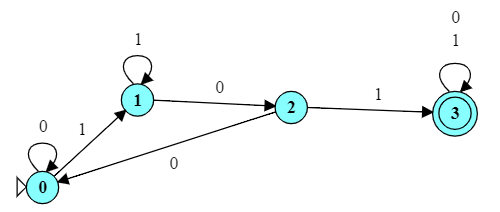
We have previously designed this FA to accepts strings that contain 101.

Design a Turing machine for the same language

Reveal

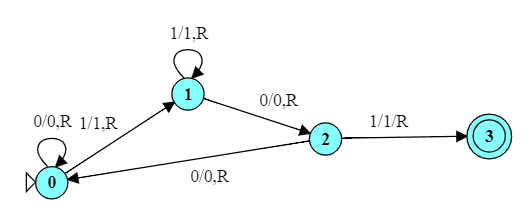
Note that we don't need transitions out of the accept state, because the TM halts as soon as we reach an accept state.

2.2 Ends with 101

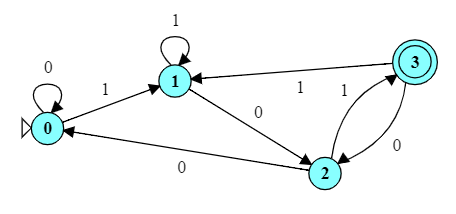Here is a FA for accepting strings that end with 101.

In this automaton, we can enter the accepting state many times (e.g., 101010) but only accept the string if we are in the accepting state AND have processed all of the input.

Design a TM to accept the same language.

Reveal

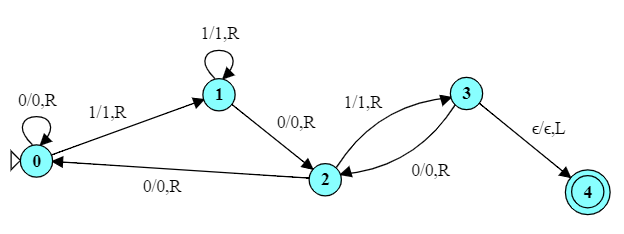
Here we have to be a bit more clever about the accept condition. Because this TM works strictly left to right, we accept if we have just seen 101 and are not looking at a blank.

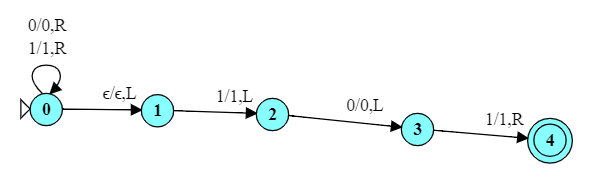
But there's a simpler, arguably more "Turing-machine-style" way to do this.

2.3 $0^n1^n$

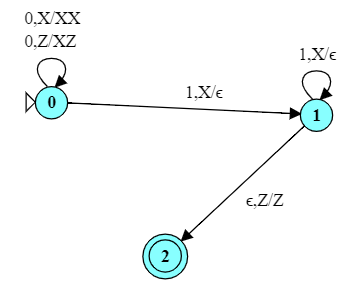
Now let's consider a context-free language.

Consider the language of all strings of the form $0^n1^n$, i.e., some number of zeros followed by an equal number of ones. This is a typical "counting" problem for a PDA, as shown to the right.

Design a TM for this language.

Reveal

The TM does not use a stack, but we achieve much the same by "matching" symbols.

3 Recognizing TMs

Use a combination of inspection and of running test cases on each of the following Turing machines to determine what it does.

3.1 Recognizing the Language Accepted by a TM

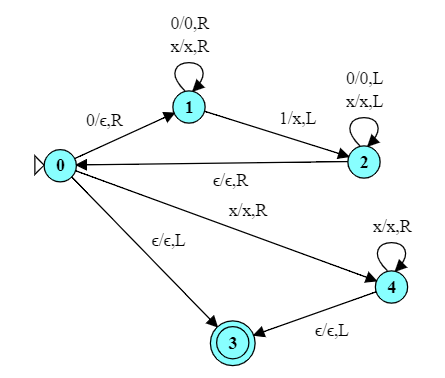
What language does this TM accept?

Reveal

All strings over {0, 1} in which the number of times a 0 is followed immediately by a 1 is odd.

This is actually a regular language. (The RE would be $1*00*11*(00*11*00*11*)*$.) You might have noticed that the TM never changes a symbol on its tape and that it processes the input on the tape in a strict left-to-right progression. In effect, all of the work is done in the TM's controller, and that controller is a DFA.

3.2 Recognizing the Function Computed by a TM

Often we think of TMs not so much as acceptors of languages as computers of functions. The input to the function is the initial content of the tape and the output is the final content of the tape when the TM reaches an accepting state.

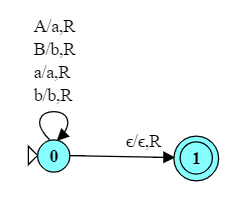
What is the function computed by this TM when presented with inputs over the language {a,b}* ?

Reveal

If computes the "lower-case" equivalent of a string over {a, b, A, B}.

3.3 TMs as Functions 2

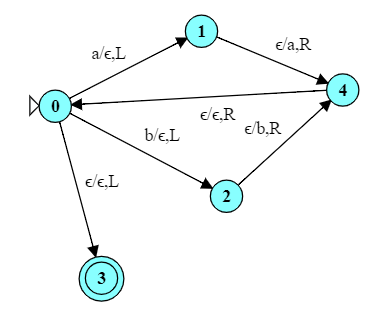
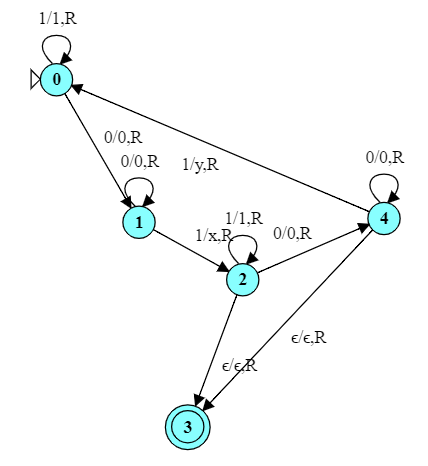
What is the function computed by this TM?

Reveal

It shifts all of the characters on the right of its starting position one step to the left, overwriting whatever character the head was originally positioned over.

3.4 TMs as Functions 3

What is the function computed by this TM?

Answer

It shifts all of the characters on the right of its starting position one step to the left, overwriting whatever character the head was originally positioned over. This time, however, we made use of a couple of JFlap shortcuts:

• ~ denotes "any character" in input, or "whatever character was just read" in output.

• characters }v denotes the "storage" of a single symbol in a "variable". In section 8.3.1 of your textbook, this is called "storage in the state" and, while a convenient programming style for TMs, has no effect on the power of a TM to recognize various languages.

  Notice how it reduces the number of explicitly drawn states, by relieving us of the necessity of separately rendering "symmetric" treatment of different possible input characters.

3.5 TMs as Functions 4

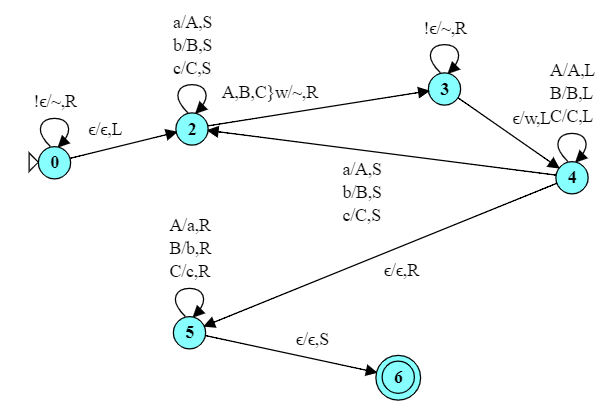
What is the function (over the input language $\{a,b\}^*$) computed by this TM?

Reveal

This is sort of a failed attempt at a palindrome generator. Given an input string over {a,b}, it places an 'x' at the end of the string, then writes the reverse of the input string after the 'x'.

I consider this a "failed" attempt at a palindrome generator because we had to rewrite the input string in order to remember what parts of the input had and had not yet been processed and, of course, we introduced the artificial 'x' character in the middle.

It constructs a palindrome of a string over {a,b} by appending the reverse of the input string onto the end of itself.

3.6 TMs as Functions 5

What is the function (over the input language $\{a,b\}^*$) computed by this TM?

Reveal

It constructs a palindrome of a string over {a,b} by appending the reverse of the input string onto the end of itself. Here we have strung together three of our previous TMs:

1. The "failed" palindrome generator that replaced the a's and b's in the original input by their upper-case equivalents and left an 'x' in the middle.

2. Our TM to convert strings over {a,b,A,B} to all-lowercase.

3. Our TM to shift everything to the right of our starting point one step to the left, to overwrite the 'x' left in the middle of the string.

Try running this one yourself on various strings over {a,b} to see that it works.

This is a good illustration of how, just as in programming, we can combine separately composed TM "functions" to achive a more complicated overall calculation.

In fact, we can be more explicit about our re-use by using another JFlap shortcut, "building blocks". We can insert any previously defined TM as a single "state" in a new one. Here I have inserted our "shiftLeft" TM from earlier (between states q6 and q8).

• A building block state connects incoming transitions to the start state of the inserted TM.
• A building block state connects outgoing transitions to (all) final states of the inserted TM.

4 Turing Machines as Language Acceptors

Earlier we saw ways to use TMs to accept languages that we had seen with earlier, less powerful automata.

Next, we can consider problems that could not be solved using the automata we have had before.

4.1 $0^n1^n2^n$

Design a TM to recognize the language of strings of the form $0^n1^n2^n$.

(Although $0^n1^n$ is a CFL and can be recognized by a pushdown automaton, $0^n1^n2^n$ is not context-free and requires a more powerful approach.)

4.2 $\alpha c\alpha$ where $\alpha \in \{a,b\}*$

4.2.1 Basic Implementation

Consider the problem of designing a TM to compare two strings over $\{a,b\}$ to see if they are equal.

All input to the TM must be on the tape, so we could choose to separate the two strings by a blank, e.g.,

          aba abb                  

or by a separator character

          abacabb                  

I'm going to choose the latter.

Another way to view this machine is to say that it recognizes strings over {a,b,c} of the form

\[ \{ \alpha c\alpha | \alpha \in \{a,b\}* \}, \]

which is definitely not a CFL.

Design a TM to recognize this language:

Reveal

First, we can try to figure out an algorithmic approach for doing this

Then we can try to design a TM to carry out this approach.

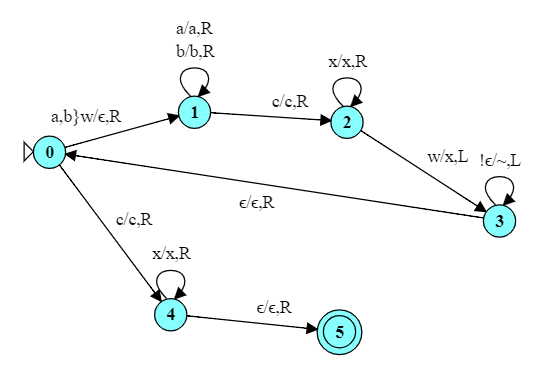
Things of note:

• q0 q1 q2 q3 When we see an 'a' in the first string, we run forward to the second string, look for a matching 'a', and mark it as having been processed.

• q3 q0 return to the beginning of (remainder of the) the first string

• q0 q4 q5 q3 When we see a 'B' in the first string, we run forward to the second string, look for a matching 'B', and mark it as having been processed.

• q0 q6 q7 When all characters in the first string have been matched, scan the second string to make sure there are no characters left over.

Using Shortcuts

Looking at the previous TM, you can see a symmetry between the branches used to handle matching and 'a' and the branch to used to handle matching a 'b'.

We can use a "state variable" (w) to reduce the need for separate branches.

We can also simplify the transitions that simply move in one direction until we hit a specific character by using ! and ~.

4.2.2 Using Multiple Tapes

We can get an even simpler (IMO) TM by using multiple tapes.

Solve the same problem using a multi-tape TM.

Reveal

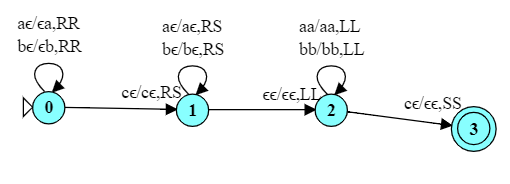
The procedure in this case is:

1. Copy the first string onto the second tape.

   At the end of this procedure, the head of the first tape will be pointing at 'c', the head of the second tape just past the end of the copied first string.

2. Leave the 2nd tape head where it is, and move the first tape head to the right until we hit the end of the second string.

3. Now start moving to the left, comparing corresponding characters in the two strings. If they match we keep going. If they don't match, we fail.

   If we reach the beginning of both strings with all matching, we accept.

5 Turing Machines as Functions

5.1 Unary Form Integer Increment

Suppose that a tape contains an integer $k$ in unary form (i.e., a string of 1's, where the value of the integer is the length of the string. Construct a TM to replace its input by the value of the function $f(k) = k+1$.

5.2 Unary Form Integer Addition

Suppose that a tape contains pair of integers $m, k$ in unary form separated by a single 'x'. Construct a TM to replace its input by the value of the function $f(m,k) = m+k$.

Reveal

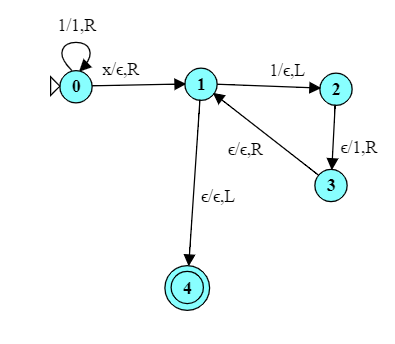
All we need to do is to remove the 'x' separating the two numbers.

Again, we could use Building Blocks to simplify this slightly.

5.3 Binary Addition - Multitape

Suppose that a TM has three tapes with a pair of integers $m, k$ in conventional binary form on tapes 1 and 2. Assume that m and k have the same number of binary digits. Construct a TM to compute the function $f(m,k) = m+k$, writing the output to the third tape.

For example, given the input tapes:

□	1	□	□	□
□	1	1	1	□
□	□	□	□	□

we would expect the output

□	1	□	□	□	□
□	1	1	1	□	□
□	1	1	1	1	□

Reveal

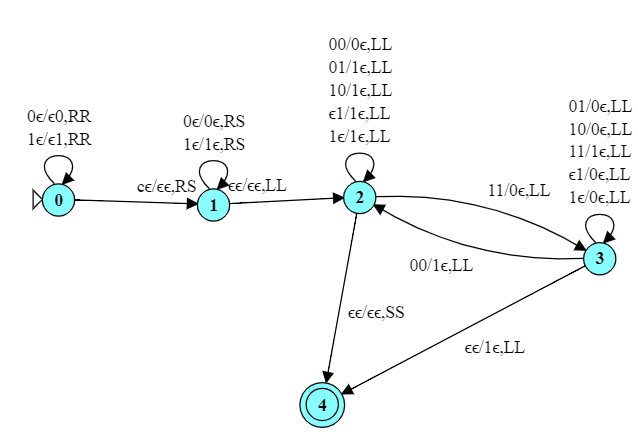
q0 shifts both input tape heads to the far right of the numbers.

q1 implements the logic of addition of binary digits where there is no "carry" from a previous step.

q2 implements the logic of addition of binary digits where there is a "carry" from a previous step.

              You can see, for example, that we go to q2 from q1 when both numbers have a '1'.                          

q3 is the final state reached when we have processed all digits in both input numbers.

Try executing this TM on inputs of your own.

This is a case where using the multiple tapes definitely simplifies the procedure. My own solution to the same problem using a single tape requires more than 30 states.

© 2016-2021, Old Dominion Univ.

Design Calculator Using Turing Machine and Jflap

Source: https://www.cs.odu.edu/~zeil/cs390/latest/Public/turing-jflap/index.html

Share this post